PARÁBOLA:
Aunque la definición original de la parábola es la relativa a la sección de un cono recto por un plano paralelo a su directriz, actualmente es más común definir la parábola como un lugar geométrico:
|
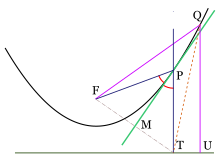
De esta forma, una vez fija una recta y un punto se puede construir una parábola que los tenga por foco y directriz de acuerdo a la siguiente construcción. Sea T un punto cualquiera de la recta directriz. Se une con el foco dado F y a continuación se traza la mediatriz (o perpendicular por el punto medio) del segmento TF. La intersección de la mediatriz con la perpendicular por T a la directriz da como resultado un punto P que pertenece a la parábola. Repitiendo el proceso para diferentes puntos T se puede aproximar tantos puntos de la parábola como sea necesario.
De la construcción anterior se puede probar que la parábola es simétrica respecto a la línea perpendicular a la directriz y que pasa por el foco. Al punto de intersección de la parábola con tal línea (conocida como eje de la parábola) se le conoce como vértice de la parábola y es el punto cuya distancia a la directriz es mínima. La distancia entre el vértice y el foco se conoce como Distancia focal o Radio focal.
Lado recto
Al segmento de recta comprendido por la parábola, que pasa por el foco y es paralelo a la directriz, se le conoce como lado recto.
|
Siendo D, E los extremos del lado recto y T, U las respectivas proyecciones sobre la directriz, denotando por W la proyección del foco F sobre la directriz, se observa que FEUW y DFWT son cuadrados, y sus lados miden FW=2FV. Por tanto el segmento DE es igual a 4 veces el segmento FV (la distancia focal).
Las tangentes a la parábola que pasan por los extremos del lado recto forman ángulos de 45° con el mismo, consecuencia de que FEUW yDFWT sean cuadrados, junto con la construcción mencionada en la sección anterior. Además, tales tangentes se cortan en la directriz de forma perpendicular, precisamente en el punto de proyección W del foco, propiedades que pueden ser aprovechadas para construir una aproximación geométrica del foco y la directriz cuando éstos son desconocidos.
Semejanza de todas las parábolas
Dado que la parábola es una sección cónica, también puede describirse como la única sección cónica que tiene excentricidad e = 1. La unicidad se refiere a que todas las parábolas son semejantes, es decir, tienen la misma forma, salvo su escala.
Desafortunadamente, al estudiar analíticamente las parábolas (basándose en ecuaciones), se suele afirmar erróneamente que los parámetros de la ecuación cambian la forma de la parábola, haciéndola más ancha o estrecha. La verdad es que todas las parábolas tienen la misma forma, pero la escala (zoom) crea la ilusión de que hay parábolas de formas diferentes.
Un argumento geométrico informal es que al ser la directriz una recta infinita, al tomar cualquier punto y efectuar la construcción descrita arriba, se obtiene siempre la misma curva, salvo su escala, que depende de la distancia del punto a la directriz.
Tangentes a la parábola
Un resultado importante en relación a las tangentes de una parábola establece:
|
En lo sucesivo, F denotará el foco de una parábola, P un punto de la misma y T su proyección sobre la directriz. Retomando la construcción dada para encontrar puntos de una parábola, seaMP la mediatriz del triángulo FPT, el cual es isósceles y por tanto biseca al ángulo FPT. Lo único que hay que verificar ahora es que MP también es la tangente en el punto P. Sea Q otro punto de la parábola y sea U su proyección en la directriz.
Puesto que FQ=QU y QU<QT, entonces FQ<QT. Dado que esto es cierto para cualquier otro punto de la parábola, se concluye que toda la parábola está de un mismo lado de MP, y como la desigualdad es estricta, no hay otro punto de la parábola que toque a la recta MP, esto quiere decir que MP es la tangente de la parábola en P.
Una parábola cuyo vértice está en el origen y su eje coincide con el eje de las coordenadas, tiene una ecuación de la forma y=ax2 donde el parámetro a especifica la escala de la parábola, incorrectamente descrita como la forma de la parábola, ya que como se dijo antes, todas las parábolas tienen la misma forma. Cuando el parámetro es positivo, la parábola se abre «hacia arriba» y cuando es negativo se abre «hacia abajo».
Si bien, la expresión en forma de ecuación no fue posible hasta el desarrollo de la geometría analítica, la relación geométrica expresada en la ecuación anterior ya estaba presente en los trabajos de Apolonio, y se bosquejará a continuación usando notación moderna.
Tomando nuevamente la definición de parábola como sección de un cono recto de forma paralela a la directriz, sea V un punto en el eje y sea QV perpendicular al eje. (QV corresponde al valor xen la versión analítica y PV al valor y). Considerando la sección circular que pasa por Q y es paralela a la base del cono, obtenemos H, K paralelos a B y C.
Por el teorema de potencia de un punto:
.
Al ser PM paralela a AC, los triángulos HVP, HKA y BCA son semejantes y así:
.
Usando nuevamente los paralelismos:
.
Despejando HV y VK para sustituir en la fórmula de QV² resulta en
.
Pero el valor de  es una constante pues no depende de la posición de V, por lo que haciendo
es una constante pues no depende de la posición de V, por lo que haciendo
 es una constante pues no depende de la posición de V, por lo que haciendo
es una constante pues no depende de la posición de V, por lo que haciendoarroja la expresión moderna y=ax².
Aplicando una sustitución de coordenadas podemos obtener ahora la ecuación de una parábola vertical para cualquier posición de su vértice.
|
agrupando los términos y reordenando se obtiene una forma equivalente:
|
Si la parábola es horizontal, se obtienen ecuaciones similares pero intercambiando y por x y viceversa. Así tendríamos:
|
ELIPSE:
La elipse posee un «eje mayor», trazo AB (que equivale a  ), y un «eje menor», trazo CD (que equivale a
), y un «eje menor», trazo CD (que equivale a 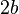 ); la mitad de cada uno de esos ejes recibe el nombre de «semieje», de tal manera que se los denomina «semieje mayor» y «semieje menor», respectivamente.
); la mitad de cada uno de esos ejes recibe el nombre de «semieje», de tal manera que se los denomina «semieje mayor» y «semieje menor», respectivamente.
 ), y un «eje menor», trazo CD (que equivale a
), y un «eje menor», trazo CD (que equivale a 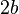 ); la mitad de cada uno de esos ejes recibe el nombre de «semieje», de tal manera que se los denomina «semieje mayor» y «semieje menor», respectivamente.
); la mitad de cada uno de esos ejes recibe el nombre de «semieje», de tal manera que se los denomina «semieje mayor» y «semieje menor», respectivamente.Sobre el «eje mayor» existen dos puntos  y
y  que se llaman «focos».
que se llaman «focos».
 y
y  que se llaman «focos».
que se llaman «focos».El punto  es uno que pertenezca a la «elipse».
es uno que pertenezca a la «elipse».
 es uno que pertenezca a la «elipse».
es uno que pertenezca a la «elipse».Puntos de una elipse
Si F1 y F2 son dos puntos del plano y d es una constante mayor que la distancia F1 F2, un punto Q pertenecerá a la elipse, si:
donde  es el semieje mayor de la elipse.
es el semieje mayor de la elipse.
 es el semieje mayor de la elipse.
es el semieje mayor de la elipse.Ejes de una elipse
Eje mayor (2 a) es la distancia mayor entre dos puntos adversos. En la figura, longitud del segmento AB.
La medida a es la mitad del eje mayor, o sea es el semieje mayor. La distancia del centro de la elipse al punto A o al punto B.
La medida a es la mitad del eje mayor, o sea es el semieje mayor. La distancia del centro de la elipse al punto A o al punto B.
El resultado constante de la suma de las distancias de cualquier punto a los focos equivale al eje mayor.
Obsérvese que d(AF2) + d (AF1) = d(AF2) + d (BF2)= AB
Obsérvese que d(AF2) + d (AF1) = d(AF2) + d (BF2)= AB
La medida b es la mitad del eje menor, o sea es el semieje menor, la distancia del centro al punto C o al punto D.
Ecuaciones de la elipse
La ecuación de una elipse en coordenadas cartesianas, con centro en el origen, es:
donde a > 0 y b > 0 son los semiejes de la elipse (a corresponde al eje de las abscisas, b al eje de las ordenadas). El origen O es la mitad del segmento [FF']. La distancia entre los focos FF' se llama distancia focal y vale 2c = 2ea, siendo e la excentricidad y a el semieje mayor.
Si el centro de la elipse se encuentra en el punto (x1, y1), la ecuación es:
En coordenadas polares con origen en un de sus focos la ecuación de la elipse es:
En coordenadas polares con origen en su centro la ecuación de la elipse es:
La ecuación paramétrica de una elipse con centro en (h,k) es:
con  no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre α y θ es
no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre α y θ es
 no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre α y θ es
no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre α y θ es-
 .
.
Área interior de una elipse
El área de la superficie interior de una elipse es:
Siendo a y b los semiejes.
Longitud de una elipse
El cálculo del perímetro de una elipse requiere del cálculo de integrales elípticas de segunda especie.
Sin embargo, el matemático Ramanujan ideó una ecuación más simple que se aproxima razonablemente a la longitud de la elipse, pero en grado menor que la obtenida mediante integrales elípticas. Ramanujan, en su formula, entre otros valores utiliza el “semieje mayor” y el “semieje menor”. Ecuación de la longitud de una elipse:
Propiedades notables
La elipse goza de ciertas propiedades asociadas a sus componentes, como se puede ver en Analogía de Michelson y Morley.
La elipse como cónica
La elipse surge de la intersección de una superficie cónica con un plano, de tal manera que la inclinación del plano no supere la inclinación de la recta generatriz del cono, consiguiendo así que la intersección sea una curva cerrada. En otro caso el corte podría ser una hipérbola o una parábola. Es por ello que a todas estas figuras bidimensionales se las llama secciones cónicas o simplemente cónicas.
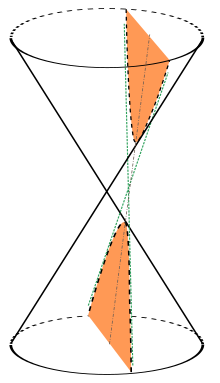
HIPÉRBOLA:
Una hipérbola (del griego ὑπερβολή) es una sección cónica, una curva abierta de dos ramas obtenida al cortar un cono recto por un plano oblicuo al eje de simetría con ángulo menor que el de la generatriz respecto del eje de revolución.
Definiciones: i. Sean F y F’ dos puntos de un plano (F ii. Las rectas: La que pasa por los focos F y F’ y la recta mediatriz del segmento F’F se llaman:Ejes de simetría de la hipérbola. iii. El punto de intersección 0 de dos ejes de simetría, se llama CENTRO de la hipérbola. Los puntos A y A’ se llaman: VERTICES de la hipérbola. Ecuaciones de la hipérbolaEcuaciones en coordenadas cartesianas: Ecuación de una hipérbola con centro en el origen de coordenadas  y ecuación de la hipérbola en su forma compleja. y ecuación de la hipérbola en su forma compleja.Ecuación de una hipérbola con centro en el punto  Ejemplos: a) b) 䉅cuación de la hipérbola en su forma compleja Una hipérbola en el plano complejo es el lugar geométrico formado por un conjunto de puntos 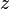 , en el plano , en el plano  ; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias ; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias 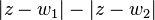 , a dos puntos fijos llamados focos , a dos puntos fijos llamados focos y y  , es una costante positiva igual al doble de la distancia (osea , es una costante positiva igual al doble de la distancia (osea  ) que existe entre su centro y cualesquiera de sus vértices del eje focal. ) que existe entre su centro y cualesquiera de sus vértices del eje focal.La ecuacion queda: 
TEOREMA: La ecuación de la hipérbola centrada en el origen y cuyos focos están en los puntos F’(0, -c) y F(0, c) viene dada por:
La demostración es similar a la anterior, se deja por lo tanto como ejercicio. sección cónica. SIGA EL ENLACE: |





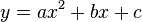 .
. .
.

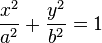





![P \approx \pi \left[3(a+b) - \sqrt{(3a+b)(a+3b)}\right]\!\,](http://upload.wikimedia.org/math/4/5/3/4531867e543bc27be7c45f80a7599da1.png)


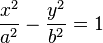
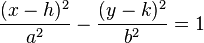

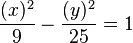



No hay comentarios:
Publicar un comentario